Percent Error Calculator
By entering the accepted value and the measured value, the calculator automatically applies the correct formula and shows the percent error clearly.
What is a Percent Error?
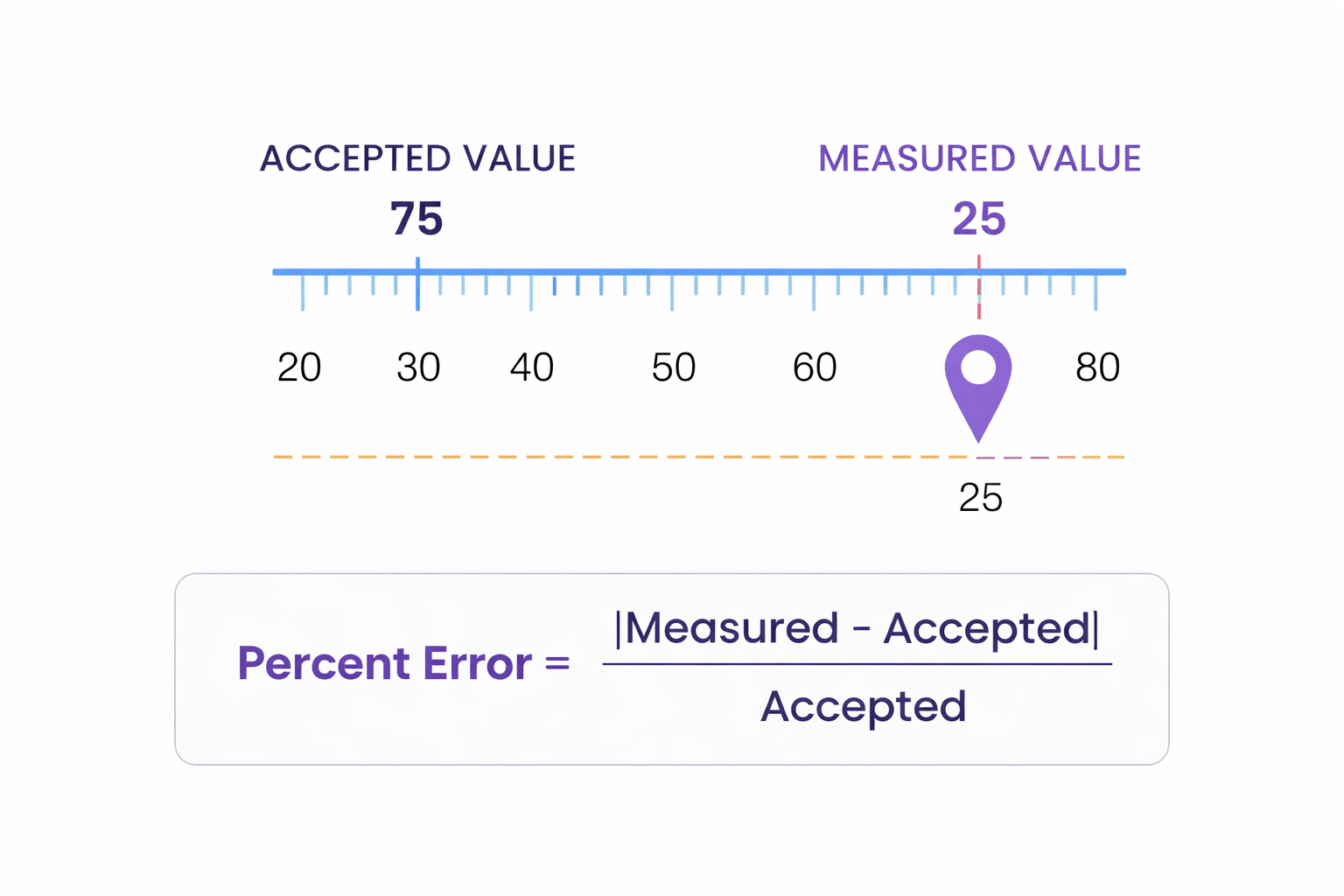
Percent error is a way to express how far a measured value deviates from the accepted or true value, written as a percentage. Instead of just showing the difference between two numbers, percent error puts that difference into context by comparing it against the accepted value. This makes it easier to judge accuracy across different scales and measurements.
A smaller percent error means the measured value is closer to the accepted value, indicating higher accuracy. A larger percent error shows a bigger deviation, which may point to experimental mistakes, faulty measurements, or real-world variability. Understanding percent error is essential in scientific analysis because it helps evaluate the reliability of results rather than just the raw numbers.
Table of Contents
How Percent Error is Calculated?
It is calculated using a standard formula that compares the difference between a measured value and an accepted value relative to the accepted value. While the formula itself is simple, understanding each part of it is essential for correct interpretation and accurate results.
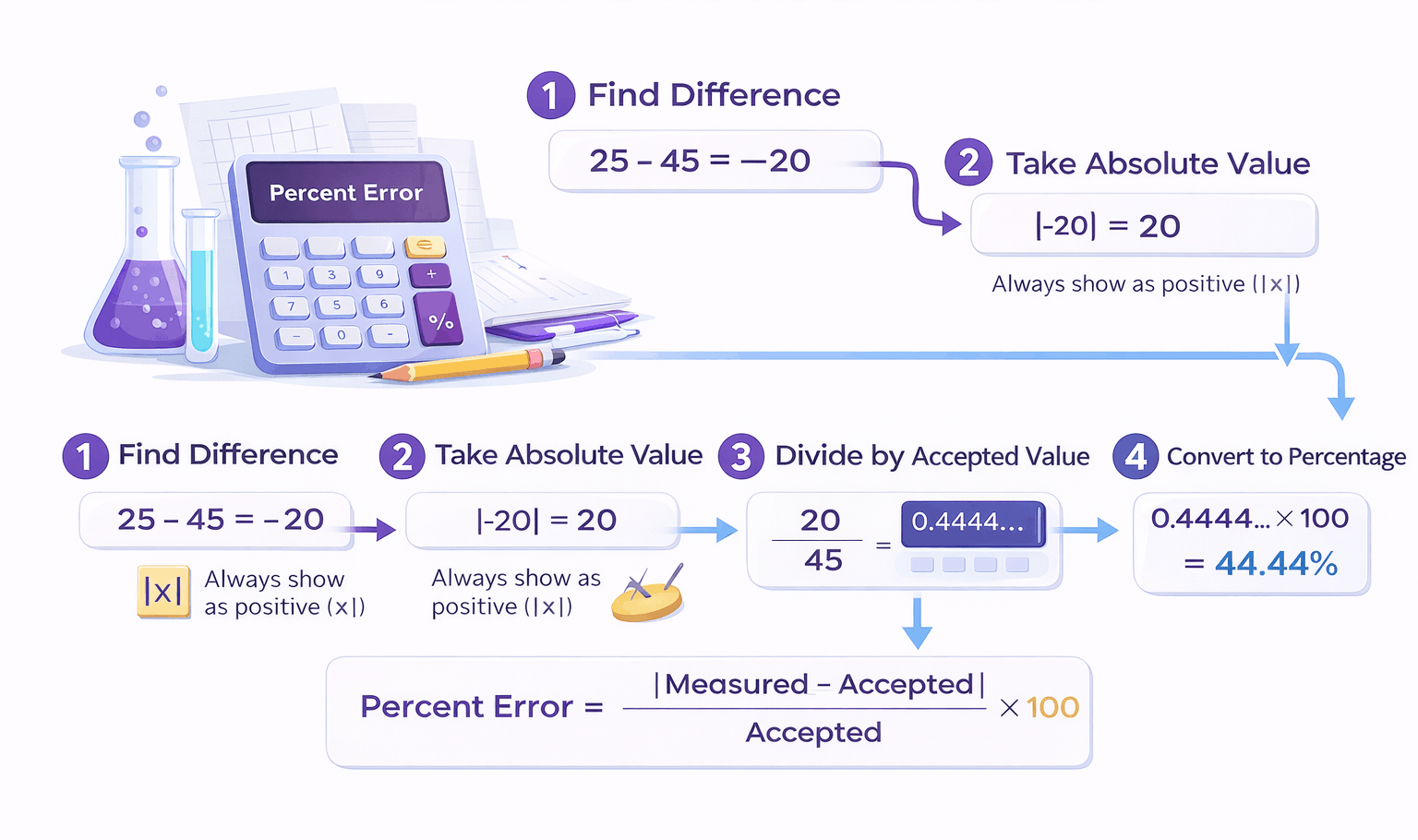
The calculation begins by subtracting the accepted value from the measured value. This step determines how far the measurement deviates from the expected result. Because measurements can be either higher or lower than the accepted value, this difference may be positive or negative. To avoid confusion and ensure consistency, the absolute value of this difference is used. This means the calculation focuses on the size of the error rather than its direction.
Once the absolute difference is found, it is divided by the accepted value. This step normalizes the error, allowing it to be compared across different scales and units. Finally, the result is multiplied by 100 to convert it into a percentage. This percentage represents the percent error.
Understanding this process helps users interpret results correctly. For example, a percent error of 2% means the measured value differs from the accepted value by 2% of the accepted value. A percent error of 50% indicates a much larger deviation, while a percent error above 100% means the difference exceeds the accepted value itself.
A Percent Error Calculator automates this entire process, ensuring the formula is applied correctly every time. This is especially important when dealing with decimals, scientific notation, or repeated calculations where manual errors are more likely.
Why Percent Error Matters
Because it provides meaningful context for measurements. Raw numbers alone do not tell the full story. Knowing that a measurement is off by a certain amount is far less useful than understanding how significant that difference is relative to the expected value.
In educational settings, percent error helps students evaluate the quality of their experiments. Instead of simply determining whether an answer is right or wrong, students can analyze how close their result is to the theoretical value and reflect on possible sources of error. This encourages critical thinking and deeper understanding rather than rote memorization.
In scientific research, percent error plays a key role in validating results. Researchers rely on percent error to assess experimental accuracy, compare results across trials, and identify systematic issues in measurement techniques. Lower percent error often indicates better experimental control and higher precision.
In professional and industrial environments, percent error is used to monitor performance, maintain quality standards, and ensure compliance with specifications. Whether measuring dimensions, output, efficiency, or predictions, percent error helps quantify reliability and consistency.
By using a percent error calculator, users gain immediate insight into the accuracy of their data, allowing for faster decisions and more confident conclusions.
Percent Error In Real-World Applications
Percent error is not limited to classrooms or laboratories. It is widely used across many real-world fields where accuracy and precision are important.
In engineering, percent error is used to compare design predictions with actual performance. Engineers analyze percent error to determine whether systems are operating within acceptable tolerances. Large percent errors may indicate design flaws, manufacturing defects, or incorrect assumptions.
In manufacturing and quality control, percent error helps ensure products meet required standards. Measurements taken during production are compared against specifications, and percent error is used to determine whether deviations are acceptable or require correction.
In data analysis and forecasting, percent error is often used to evaluate predictions. Analysts compare predicted values with actual outcomes to assess model accuracy. Lower percent error indicates better predictive performance, while higher percent error highlights areas for improvement.
Even in everyday contexts such as budgeting, planning, or estimating time and resources, percent error can help evaluate how accurate an estimate was compared to the final result.
If you prefer learning visually, watch this YouTube video for a clear, step-by-step breakdown of how it’s calculated.
Common Mistakes When Calculating Percent Error
Confusing percent error with percent difference
Percent error requires a known accepted or true value, while percent difference is used when comparing two values without assuming one is correct. Using the wrong formula can lead to incorrect or misleading results.
Forgetting to use absolute value
Percent error should always be expressed as a positive percentage. Without using absolute value, the result may appear negative, which does not align with standard scientific definitions.
Dividing by the wrong value
The difference between values must always be divided by the accepted value, not the measured value. Dividing by the wrong number can significantly distort the final percent error.
Rounding too early in the calculation
Rounding numbers before completing the full calculation can introduce additional error. Calculations should be performed at full precision, with rounding applied only to the final result.
Assuming a high percent error always means failure
A large percent error does not always indicate a mistake. It may reflect natural variation, experimental limitations, or measurement constraints.
Not checking input values carefully
Entering incorrect accepted or measured values can produce misleading results. Double-checking inputs is essential for accurate percent error calculations.
Percent Error Vs Percent Difference Vs Relative Error
These three concepts are closely related and often confused, but they are used in different situations depending on what kind of comparison is being made. Understanding the difference between percent error, percent difference, and relative error is essential for choosing the correct method and interpreting results accurately in science, engineering, and data analysis.
Using the wrong metric can lead to misleading conclusions, especially when one value is assumed to be correct or when comparing two values without a known reference. The sections below explain each concept clearly and when it should be used.
Percent Error
Percent error is used when a known accepted or true value exists. It shows how far a measured value deviates from that accepted value, expressed as a percentage.
It focuses on accuracy and always uses absolute value, meaning results are shown as positive percentages. Smaller percent error indicates higher accuracy.
Percent Difference
Percent difference is used when comparing two values without assuming either one is correct. It measures how different the values are relative to their average.
This method is ideal for side-by-side comparisons but should not be used when an accepted value is available.
Relative Error
Relative error compares the difference between measured and accepted values as a ratio instead of a percentage.
It provides the same information as percent error but is commonly used in theoretical, statistical, or formula-based analysis.
Why These Distinctions Matter?
Using the correct method ensures results are interpreted accurately. Percent error checks accuracy, percent difference compares values, and relative error expresses proportional deviation. Choosing the right one prevents confusion and incorrect conclusions.
How This Percent Error Calculator Helps
This Percent Error Calculator is designed to remove complexity and provide clear, accurate results instantly. Users simply enter the accepted value and the measured value, and the calculator applies the correct scientific formula automatically.
The calculator supports a wide range of inputs, including decimals, negative numbers, and scientific notation. It also offers flexible rounding options, allowing users to control how results are displayed based on their needs.
By clearly presenting the accepted value, measured value, and percent error together, the calculator makes results easy to understand and interpret. This clarity is especially valuable for students learning the concept for the first time and for professionals who need quick, reliable calculations.

Who Should Use A Percent Error Calculator
Students use percent error calculators to verify homework answers, analyze lab results, and prepare for exams. Teachers use them as teaching aids to demonstrate accuracy and error analysis concepts.
Researchers and scientists rely on percent error to evaluate experimental accuracy and compare results across trials. Engineers and technicians use it to assess system performance and measurement reliability.
Data analysts, manufacturers, and quality control professionals use percent error to monitor consistency, identify trends, and maintain standards.
Because percent error applies across so many fields, this calculator is designed to be flexible, accurate, and easy to use for everyone.
Frequently Asked Questions
Find clear answers to common questions about percent error, accuracy, and calculation concepts explained in a simple way.
What is percent error and why is it used?
Percent error measures how far a measured or observed value differs from an accepted or true value, expressed as a percentage. It is used to evaluate accuracy and understand how close a result is to what was expected.
How do you calculate percent error step by step?
Percent error is calculated by finding the difference between the measured value and the accepted value, taking the absolute value of that difference, dividing it by the accepted value, and multiplying by 100.
What is the difference between percent error and percent difference?
Percent error is used when a known accepted value exists and measures accuracy. Percent difference is used when comparing two values where neither is considered correct and measures how different they are relative to each other.
Why is percent error always shown as a positive value?
Percent error uses absolute value because it represents the size of the error, not the direction. A positive percentage makes results easier to interpret and consistent with scientific standards.
Can percent error be greater than 100 percent?
Yes, percent error can be greater than 100 percent when the difference between the measured value and the accepted value is larger than the accepted value itself.
What does a low percent error indicate?
A low percent error indicates high accuracy, meaning the measured value is very close to the accepted or true value.
When should percent error not be used?
Percent error should not be used when there is no accepted or true value available. In such cases, percent difference is more appropriate.
How is relative error different from percent error?
Relative error expresses the size of the error as a ratio instead of a percentage. Percent error is simply relative error multiplied by 100.
Can this percent error calculator handle decimals and scientific notation?
Yes, this percent error calculator supports decimals, negative values, large numbers, small values, and scientific notation for accurate calculations.
Is this percent error calculator suitable for school and college-level work?
Yes, the calculator follows standard academic definitions and formulas, making it suitable for middle school, high school, and college-level assignments.
Some of our popular calculators: