Mean Value Theorem Calculator (MVT) with Steps

This Mean Value Theorem Calculator quickly finds the value of c where the derivative equals the average rate of change on a given interval. It applies core calculus principles automatically, making complex problems simple to solve.

Enter your function and interval to compute endpoint values, calculate the secant slope, differentiate the function, and solve for the point that satisfies the theorem. The tool follows the formal definition used in university calculus courses.

Table of Contents

What Is the Mean Value Theorem (MVT)?

The Mean Value Theorem (MVT) is a central result in differential calculus. It states that if a function is continuous on a closed interval $[a, b]$ [a,b] and differentiable on the open interval $(a, b)$ (a,b), then there exists at least one number $c$ c in that interval such that: $f'(c) = \frac{f(b) – f(a)}{b – a}$

In simple language, this means that at some point between $a$ a and $b$ b, the slope of the tangent line equals the slope of the secant line.

According to MIT OpenCourseWare, the MVT formally connects average rate of change with instantaneous rate of change and serves as the foundation for many advanced calculus results. The theorem is explained in their Single Variable Calculus materials at https://ocw.mit.edu.

Why the Mean Value Theorem Matters in Calculus

The MVT is not just a formula. It guarantees that if something changes over time, there must be at least one moment when the instantaneous rate equals the overall average rate.

A 2013 study published in the Journal of Mathematical Behavior found that students who connect graphical interpretations of secant and tangent lines develop stronger conceptual understanding of derivatives. This reinforces why computational tools combined with theory improve learning.

In physics, the theorem explains why a car traveling 100 miles in 2 hours must have been moving exactly 50 mph at some moment. In economics, it supports marginal cost and marginal revenue analysis.

The MVT builds the bridge between theoretical derivatives and real-world rate behavior.

How This Mean Value Theorem Calculator Works

This mean value theorem calculator follows the formal steps required by calculus theory:

Evaluates the function at $a$ a and $b$ b
Computes the average rate of change
Finds the derivative $f'(x)$
Solves $f'(c) = \frac{f(b) – f(a)}{b – a}$
Returns valid solutions inside the interval

If continuity or differentiability conditions fail, the calculator identifies the issue clearly.

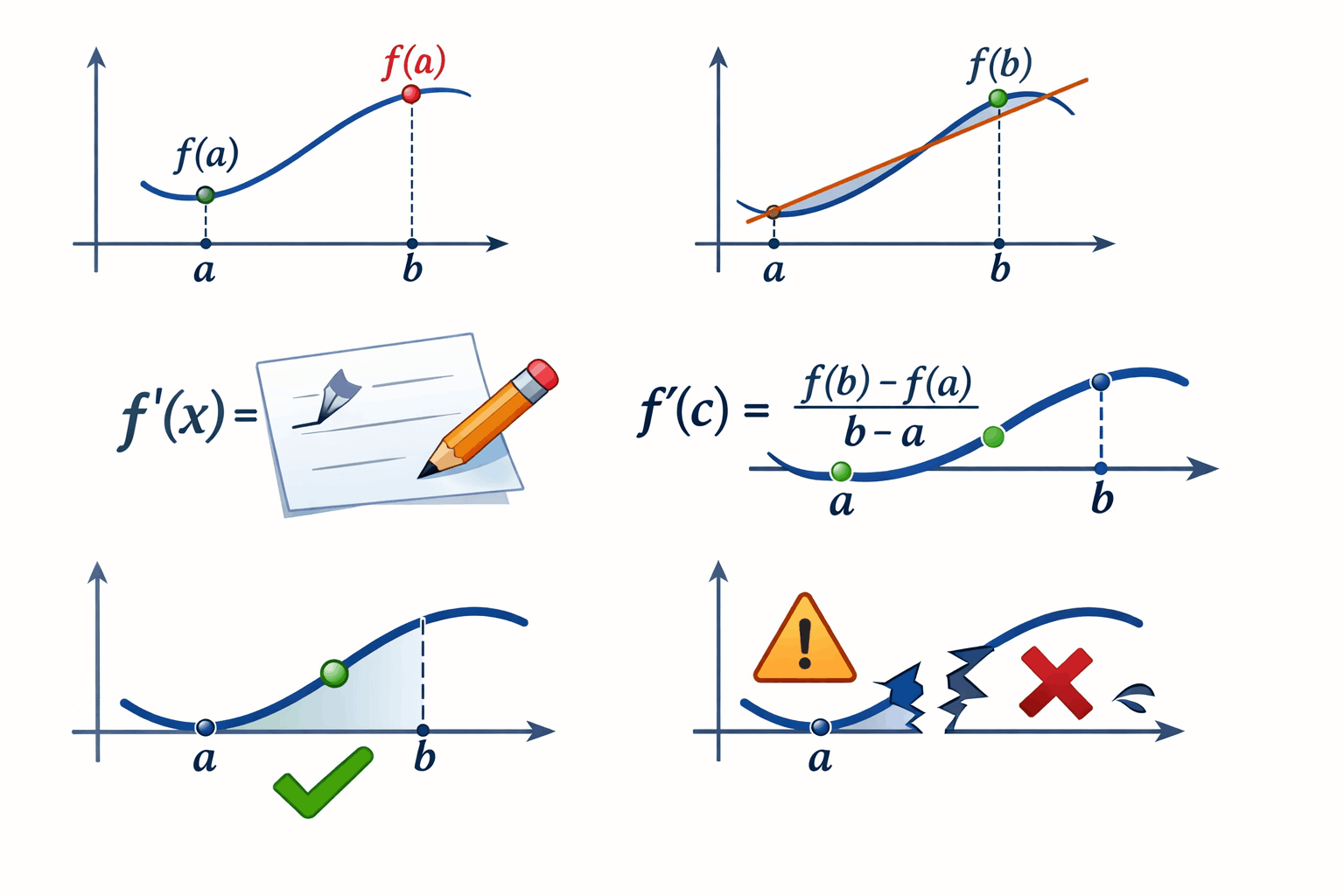
How This Mean Value Theorem Calculator Works

This mirrors the structured approach taught in university calculus courses.

Mathematical Conditions Behind the MVT

For the Mean Value Theorem (MVT) to apply, two conditions must hold:

Continuity on the closed interval
Differentiability on the open interval

Continuity ensures no breaks or jumps. Differentiability ensures no sharp corners or cusps.

According to the American Mathematical Society (AMS), Rolle’s Theorem is a special case of the MVT where endpoint values are equal. This relationship highlights how the theorem builds on earlier foundational results in calculus.

If either condition fails, the theorem does not guarantee a solution.

Step-by-Step Example

Let’s apply the theorem to:

$f(x) = x^2$ on $[1, 3]$

Step 1:
$f(1) = 1$
$f(3) = 9$

Step 2:

$\frac{9 - 1}{3 - 1} = 4$ Step 3:
$f'(x) = 2x$

Step 4:

Solve $2c = 4$

$c = 2$

The value lies inside (1, 3), so the MVT is satisfied.

The calculator performs these steps instantly.

Real-World Applications of the Mean Value Theorem

The Mean Value Theorem (MVT) is used in multiple applied disciplines:

In physics, it guarantees specific velocity values during motion intervals.
In economics, it connects average and marginal change.
In engineering, it supports rate modeling and optimization.

A 2020 study in Applied Mathematics and Computation demonstrated how derivative-based rate models are widely used in engineering simulations and financial forecasting.

Harvard University applied mathematics lectures emphasize that rate-of-change principles form the basis of predictive modeling and optimization theory.

The MVT provides theoretical justification for these applied models.

Common Errors Students Make

Manual calculations often include:

Algebra mistakes
Incorrect derivative rules
Ignoring interval restrictions
Accepting extraneous solutions
Forgetting theorem conditions

A 2015 mathematics education study at the University of Michigan identified algebraic manipulation errors as one of the most common causes of incorrect calculus solutions.

Using a reliable computational tool reduces these risks while reinforcing conceptual understanding.

Supported Function Types

A comprehensive mean value theorem calculator should support:

Polynomial functions
Rational expressions
Exponential functions
Logarithmic functions
Trigonometric functions
Composite functions

It should also handle decimals, fractions, negative intervals, and multiple solutions accurately.

These capabilities align with standard university-level calculus requirements.

Frequently Asked Questions

What does a mean value theorem calculator do?

A mean value theorem calculator computes the value of $c$ where the derivative equals the average rate of change over a given interval, verifying continuity and differentiability before solving.

What is the Mean Value Theorem in simple terms?

The Mean Value Theorem states that if a function is continuous and differentiable on an interval, there is at least one point where the instantaneous rate equals the average rate over that interval.

Can there be more than one value of $c$ ?

Yes. Depending on the function’s shape, multiple points inside the interval may satisfy the Mean Value Theorem equation.

What happens if the function is not continuous?

If the function is not continuous on the closed interval, the Mean Value Theorem does not apply and no guaranteed solution exists.

What happens if the function is not differentiable?

If the function is not differentiable inside the interval, the theorem cannot guarantee a valid value of $c$ .

Can this calculator handle trigonometric functions?

Yes. The calculator supports trigonometric, exponential, logarithmic, polynomial, and rational functions.

Does it support decimal intervals?

Yes. Decimal and fractional endpoints are fully supported with accurate computation.

Is this useful for exam preparation?

Yes. It follows the exact definition taught in standard calculus textbooks and university courses.

Why is the MVT important in calculus?

The Mean Value Theorem connects derivatives to real-world rates of change and supports advanced results like Taylor’s Theorem and error estimation.

Is the mean value theorem calculator accurate?

The calculator follows the formal mathematical definition of the Mean Value Theorem and computes derivatives and solutions using precise symbolic or numerical methods.

Summary

The Mean Value Theorem Calculator automates the full theorem process: checking conditions, computing average rate of change, differentiating functions, and solving for valid interior points. By combining formal calculus theory with precise computation, it supports both conceptual understanding and practical problem solving.

Some of our other calculators: